BAB 6 Koordinat Kartesius, Vektor, dan Persamaan Bidang dalam Ruang Dimensi BAHAGIAN 1

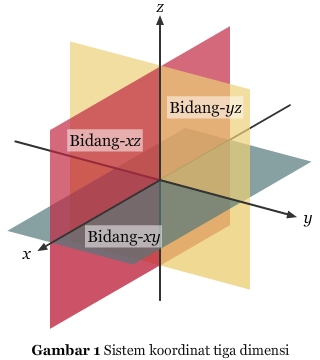
Gambar 1
Mungkin sebelumnyai, kita telah memberikan perhatian utama pada sistem koordinat dua dimensi. Akan tetapi dalam mempelajari kalkulus kita akan memerlukan sistem koordinat tiga dimensi.
Kita dapat membangun sistem ini dengan membuat sumbu-z yang memotong tegak lurus sumbu-x dan sumbu-z pada titik asal, seperti yang ditunjukkan Gambar 1. Jika kita memasangkannya, sumbu-sumbu tersebut akan membentuk tiga bidang koordinat: bidang-xy, bidang-xz, dan bidang-yz. Ketiga bidang koordinat ini akan memisahkan ruang menjadi delapan oktan. Oktan pertama berisi titik-titik yang semua koordinatnya positif.

Dalam sistem tiga dimensi ini, suatu titik P dalam ruang ditentukan dengan tripel berurutan (x, y, z), dimana x, y, dan z dijelaskan sebagai berikut.
  • x = jarak langsung dari bidang-yz ke P
  • y = jarak langsung dari bidang-xz ke P
  • z = jarak langsung dari bidang-xy ke P
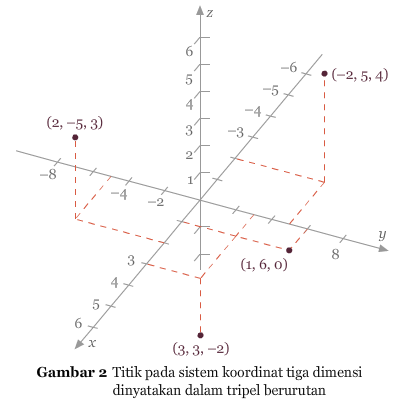
Beberapa titik ditunjukkan dalam Gambar 2 berikut.
Gambar 2

. Dengan melakukan ini, kita akan memperoleh rumus jarak antara dua titik (x1, y1, z1) dan (x2, y2, z2).
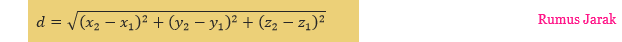
Rumus Jarak



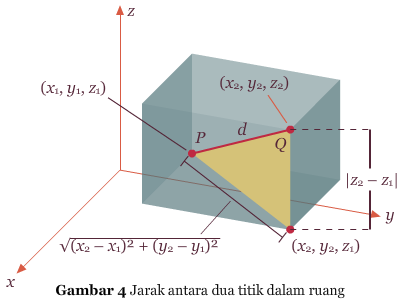
Gambar 4













Hasil Kali Silang Dua Vektor

Hasil kali silang (hasil kali vektor atau cross product), u x v untuk  u = <u1, u2,u3> dan v = <v1, v2,v3> didefinisikan sebagai:
 

Komentar

Posting Komentar

Postingan populer dari blog ini

persamaan parametrik dan vektor pada bidang

Gambar
A. Persamaan Parametrik  Fungsi parametrik adalah fungsi yang dipengaruhi oleh paramater tertentu. misalnya ” t” . yang biasanya  y=f(x) menjadi x=f(t) dan y=g(t) . Perlunya menggunakan fungsi parametrik adalah karena suatu kurva berubah posisi koordinatnya (x,y) lebih karena dipengaruhi oleh faktor “t”. Sehingga kadang kurva terlihat begitu rumit, model kurva ini dibagi menjadi 4 kelompok 1. kurva tertutup tifdak sederhana 2. kurva tertutup sederhana 3. kurva tidak tertutup tidak sederhana 4. kurva tidak tertutup tidak sederhana Berikut ini contoh sebuah fungsi parametrik dan bagaimana membuat gambarnya Untuk membuat gambarnya, lebih mudah untuk membuat tabel 3 kolom seperti dibawah ini kemudian baru digambar. Buatlah titik-titik koordinat (x,y) hasil dari memasukkan nilai “t” ke dalam persamaan f(t) dan g(t), kemudian dilanjutkan dengan membentuk kurva yang mulus Terlihat dari gambar di atas, adalah sebuah kurva parabola. Dan kita bisa mengetah
Terus membaca

BAB I KEDUDUKAN TITIK DAN KURVA PADA KOORDINAT CARTESIUS

Gambar
BAB I KEDUDUKAN TITIK DAN KURVA PADA KOORDINAT CARTESIUS Sebelum kita membahas titik dan kurva pada sistem koordinat cartesius, kita harus tau dulu nih bagaimana konsep dari titik, bagaimana sifatnya, lalu bagaimana kedudukannya. Berikut adalah sifat-sifat dari titik. T tik t idak mem punyai panjang, ukuran, besaran satuan, lebar maupun tinggi. Titik memiliki posisi /kedudukan/letak. Sebuah titik dilukiskan dengan tanda Noktah. Pada koordinat t itik biasanya dilambangkan dengan huruf kapital, seperti titik A, B, C, dan lain-lain. Konsep Titik pada Sumbu Koordinat Konsep titik diperkenalkan dalam geometri Euclid sebagai elemen yang tidak didefinisikan dan tidak memiliki dimensi panjang. Euclid mendefinisikan titik dalam buku I - Element yaitu “a point is that which has no part” . Geometri Euclid hanya membahas sifat titik yang diam/tetap, sedangkan geometri analitik juga menelaah sifat-sifat titik yang bergerak seperti yang terjadi di alam.
Terus membaca