persamaan parametrik dan vektor pada bidang

A. Persamaan Parametrik

Fungsi parametrik adalah fungsi yang dipengaruhi oleh paramater tertentu. misalnya ” t” . yang biasanya y=f(x) menjadi x=f(t) dan y=g(t). Perlunya menggunakan fungsi parametrik adalah karena suatu kurva berubah posisi koordinatnya (x,y) lebih karena dipengaruhi oleh faktor “t”. Sehingga kadang kurva terlihat begitu rumit, model kurva ini dibagi menjadi 4 kelompok
1. kurva tertutup tifdak sederhana

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiQC922Ghht7ZjFhtDUzNT5PwTzFY-iCd2GJd2VLxp3mxAFO59Fu_b7oR1XRW83T8RqbjQRtihQEOzcZliK8u23lE8xDzCWI2jFigV12Z1B56OSsZPcvkgMpbbRs3xX3cZLZYl16nJGvpih/s1600/e.PNG

2. kurva tertutup sederhana

Hasil gambar untuk kurva tertutup sederhana

3. kurva tidak tertutup tidak sederhana

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj89VmYBpKfJI8-PcwUOzIoLD2w3UTSevg5BFcvbCjv-OAY_JooHPpgPyGaphjq_gr51gvMvOwYAukADdrRkKpBHJLhYTUe4bDWUbhG0pFj8YYBBhEit3Ht4ELmOfOLux1zdKasDnGPqzAV/s1600/b.PNG

4. kurva tidak tertutup tidak sederhana
Hasil gambar untuk kurva terbuka tidak sederhana

Berikut ini contoh sebuah fungsi parametrik dan bagaimana membuat gambarnya

Untuk membuat gambarnya, lebih mudah untuk membuat tabel 3 kolom seperti dibawah ini kemudian baru digambar. Buatlah titik-titik koordinat (x,y) hasil dari memasukkan nilai “t” ke dalam persamaan f(t) dan g(t), kemudian dilanjutkan dengan membentuk kurva yang mulus

Terlihat dari gambar di atas, adalah sebuah kurva parabola. Dan kita bisa mengetahui persamaan parametrik di atas merupakan persamaan parabola atau bukan, dengan mengeliminasi paramater “t”. Caranya sebagai berikut

Contoh lain cara menghilangkan parameter dalam persamaan parametrik

Juga contoh berikut

Aplikasi Turunan dan Integral pada Persamaan Parametrik
Seperti halnya persamaan dalam bentuk y=f(x), maka persamaan parametrik juga bisa diturunkan dan juga diintegralkan. Akan tetapi harus mengikuti beberapa cara berikut
Penurunan Funsi Parametrik

Untuk lebih jelasnya, mari kita perhatikan contoh berikut

B.Vektor Pada Bidang

Vektor digambarkan seperti anak panah (ruas garis berarah). Panjang ruas garis menyatakan besarnya vektor dan arah anak panah menyatakan ara vektor. Selanjutnya, vektor didefenisikan sebagai berikut:

Vektor adalah himpunan ruas garis berarah yang mempunyai besar dan arah yang sama.

Suatu vektor terdiri dari panah- panah yang digambarkan, panah ini memiliki 2 ujung, yaitu titik awal (pangkal) dan titik akhir (ujung). Vektor adalah besaran yang mempunyai nilai dan arah. Dua vektor dikatakan ekuivalen jika kedua vektor tersebut memiliki besaran dan arah yang sama

Suatu vektor dapat diberi simbol dengan salah satu anggotanya sebagai wakil. Misalnya pada gambar 1, ruas ruas garis berarah itu mempunyai besar dan arah sama, maka vektor itu dapat dinyatakan dengan simbol

atau

1. Penjumlahan Vektor

Penjumlahan dua buah vektor ialah mencari sebuah vektor yang komponen-komponennya adalah jumlah dari kedua komponen-komponen vektor pembentuknya.

Dengan kata lain untuk “menjumlahkan dua buah vektor”adalah “mencari resultan”. Untuk vektor-vektor segaris, misalnya vektor A dan B dalam posisi segaris dengan arah yang sama seperti tampak pada gambar (a) berikut maka resultan (jumlah) vektor dituliskan:

R=A+B

Pada kasus penjumlahan vektor yang lain, seperti yang ditunjukkan gambar (b) diatas terdapat dua vektor yang tidak segaris yang mempunyai titik pangkal sama tetapi dengan arah yang berbeda, sehingga membentuk sudut tertentu. Untuk vektor-vektor yang membentuk sudut á , maka jumlah vektor dapat dilukiskan dengan menggunakan metode

tertentu. Cara ini disebut dengan metode jajaran genjang.

Cara melukiskan jumlah dua buah vektor dengan metode jajaran genjang sebagai berikut:

a. titik tangkap A dan B dibuat berimpit dengan memindahkan titik tangkap A ke titik tangkap B, atau sebaliknya;

b. buat jajaran genjang dengan A dan B sebagai sisi-sisinya;

c. tarik diagonal dari titik tangkap sekutu, maka A + B = R adalah diagonal jajaran genjang.

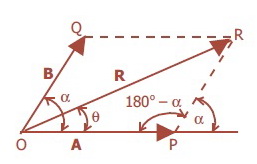
Metode Jajaran Genjang Untuk Penjumlahan Vektor

metode jajaran gejang,vektor jajar genjang

Gambar diatas menunjukkan penjumlahan dua vektor A dan B. Dengan menggunakan persamaan tertentu, dapat diketahui besar dan arah resultan kedua vektor tersebut. Persamaan tersebut diperoleh dengan menerapkan aturan cosinus pada segitiga OPR, sehingga dihasilkan:

(OR)²= (OP)²+ (PR)²– 2 (OP)(PR) cos (180^o– α)

= (OP)²+ (PR)²– 2 (OP)(PR)(–cos α)

(OR)²= (OP)²+ (PR)²+ 2 (OP)(PR)cos α

Diketahui bahwa OP = A, PR = OQ = B, OR = R, sehingga:

$R^{2}=A^{2}+B^{2}+2ABcos \alpha$

$R=\sqrt{A^{2}++B^{2}+2ABcos\alpha }$

R adalah diagonal panjang jajaran genjang, jika α lancip. Sementara itu, α adalah sudut terkecil yang dibentuk oleh A dan B.

Sebuah vektor mempunyai besar dan arah. Jadi setelah mengetahui besarnya, kita perlu menentukan arah dan resultan vektor tersebut. Arah R dapat ditentukan oleh sudut antara R dan A atau R dan B.

Misalnya sudut θ merupakan sudut yang dibentuk R dan A, maka dengan menggunakan aturan sinus pada segitiga OPR akan diperoleh:

$\frac{R}{sin(180-\alpha )}=\frac{B}{sin\Theta }=\frac{R}{sin\alpha }$

$\frac{R}{sin\alpha }=\frac{B}{sin\Theta }$

Sehingga :

$sin\Theta =\frac{Bsin\alpha }{R}$

Dengan menggunakan persamaan tersebut, maka besar sudut θ dapat diketahui.

Metode Segitiga Untuk Penjumlahan Vektor

Metode segitiga merupakan cara lain untuk menjumlahkan dua vektor, selain metode jajaran genjang. Dua buah vektor A dan B, yang pergerakannya ditunjukkan metode segitia (a)diatas, akan mempunyai resultan yang persamaannya dituliskan:

R = A + B

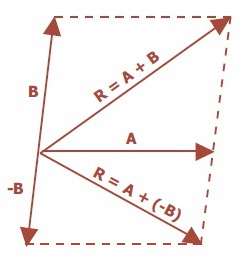
Pengurangan Vektor

Pengurangan vektor pada prinsipnya sama dengan penjumlahan, tetapi dalam hal ini salah satu vektor mempunyai arah yang berlawanan. Misalnya, vektor A dan B, jika dikurangkan maka:

A – B = A + (-B)

Di mana, –B adalah vektor yang sama dengan B, tetapi berlawanan arah.

Selisih Vektor A-B

Perkalian Vektor

1. Perkalian sebuah konstanta dengan sebuah vektor

Perkalian sebuah konstanta dengan sebuah vector

“Jika k positif maka arahnya sama dengan arah vector a”
“Jika k negatif maka arahnya berlawanan dengan vector a”

2. Perkalian dua buah vector dengan hasil berupa skalar

Operasi di atas disebut juga “dot product”

Keterangan:

a = vector a

b = vector b

θ = sudut yang dibentuk antara vector a dan vector b

3. Perkalian dua buah vector dengan hasil berupa vector lain

Keterangan:

a = vector a

b = vector b

θ = sudut yang dibentuk antara vector a dan vector b

Operasi di atas disebut juga “cross product”

Arah hasil perkalian vector a dan b selalu tegak lurus dengan bidang yang dibentuk oleh vector a dan b.

Untuk menentukan arah perkalian vector:

Kepalkan jari tangan melingkupi sumbu sambil mendorong vector a ke vector b oleh ujung-ujung jari melalui sudut terkecil, sementara ibu jari tetap tegak jadi hasil perkalian vector a dan b ditentukan oleh ibu jari.

Hasil gambar untuk menentukan vektor dengan jari

Jika kita mengetahui komponen-komponen vector yang akan kita kalikan, kita bisa menggunakan sifat-sifat perkalian silang diantara sesama vector satuan untuk mencari hasil perkalian silang antara dua vector. Sifat-sifat tersebut adalah:

i x i = j x j = k x k = 0

i x j = -j x i = k

j x k = -k x j = i

k x i = -i x k = j

Contoh 1: Representasi Vektor: Ruas-ruas Garis Berarah
Misal v merepresentasikan ruas garis berarah dari (0, 0) ke (3, 2), dan misalkan u merepresentasikan ruas garis berarah dari (1, 2) ke (4, 4). Tunjukkan bahwa u dan v ekuivalen.
Pembahasan Misalkan P(0, 0) dan Q(3, 2) menjadi titik pangkal dan titik ujung v, dan misalkan R(1, 2) dan S(4, 4) menjadi titik pangkal dan titik ujung u, seperti yang ditunjukkan Gambar 3. Kita dapat menggunakan Rumus Jarak untuk menentukan panjang PQ dan RS memiliki panjang yang sama.
1 PQ

Kedua segmen tersebut memiliki arah yang sama, karena kedua garis tersebut mengarah ke kanan atas pada garis-garis yang memiliki gradien sama.
1 mPQ

dan

Karena ruas garis berarah PQ dan RS memiliki panjang dan arah sama, kita dapat menyimpulkan bahwa kedua vektor tersebut ekuivalen. Yaitu, v dan u ekuivalen.

Contoh 1

Mengubah Persamaan Parametrik Menjadi Persamaan Kartesian

1. Ubahlah persamaan parametrik ke dalam bentuk kartesian a. x = t - 1, y = t2

b. x = 2cos t dan y = 2 sin t

Jawab

Cari Blog Ini

GEONALL